Akustik Instrumentenkunde Gehörbildung Musikgeschichte Aufnahmeprüfung kleines Lexikon
DIE UNREINEN INTERVALLE
Große und kleine
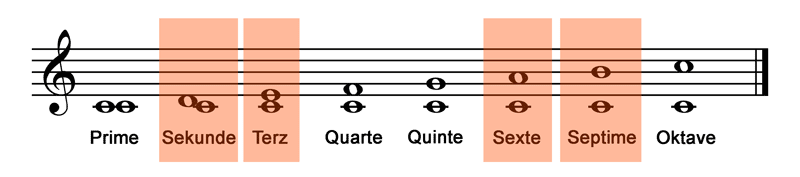
Die Intervalle, die entstehen, wenn dem Grundton der C-Dur-Tonleiter nacheinander jeweils der
nächste Tonleiterton hinzugefügt wird sind ja schon bekannt ( Intervalle allgemein ).
Wer genau hinhört, wird feststellen, dass hier aber nur große unreine Intervalle zu finden sind:
Wo bleiben denn die kleinen?
Die tauchen zum Beispiel dann auf, wenn das Ganze umgekehrt wird, wenn dem Grundton der Tonleiter nacheinander immer der nächst tiefere Tonleiterton hinzugefügt wird:
(Alle "C"s in der C-dur-Tonleiter sind Grundtöne, egal, ob der höhere oder der tiefere genommen wird.)
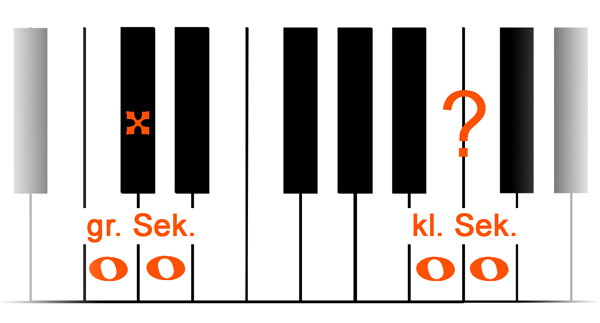
Ein Vergleich der beiden Sekunden ergibt: Zwischen den Tönen der großen Sekunde befindet sich ein Ton (x), während die Töne der kleinen Sekunde direkte Nachbarn sind (keine schwarze Taste):
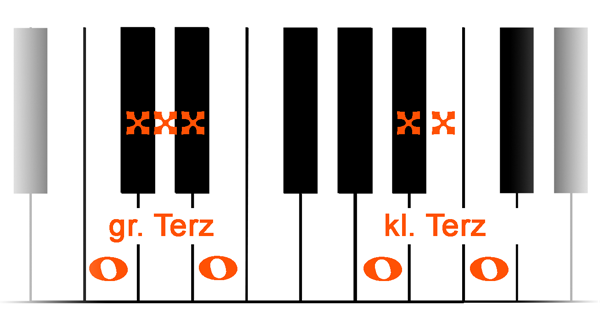
Die Töne der großen Sekunde sind also weiter voneinander entfernt als die der kleinen. Eine große Sekunde wird auch "Ganzton" genannt, eine kleine Sekunde "Halbton". Entsprechend verhält es sich mit den Terzen (gr.: 3, kl.: 2 Töne):
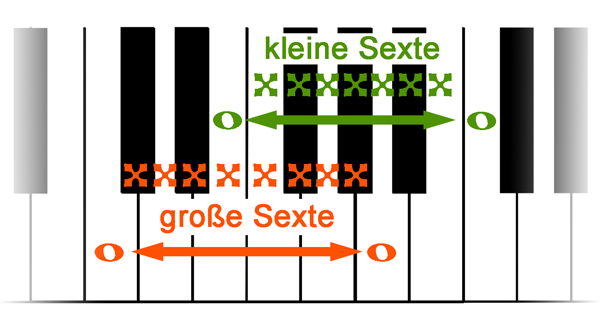
den Sexten (gr.: 8, kl.: 7 Töne):
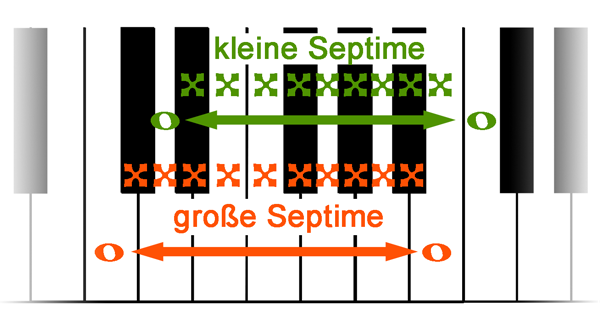
und den Septimen (gr.: 10, kl.: 9 Töne):
